Sebelum membahas permutasi akan dikenalkan terlebih dahulu notasi faktorial, yaitu : Jika n bilangan asli, maka n faktorial ditulis n ! didefinisikan sebagai berikut
n! = n (n - 1) (n - 2) (n - 3) … 3. 2. 1
Dan nol faktorial didefinisikan sebagai 0! = 1
Sebagai contoh
01. Hitunglah setiap nilai faktorial berikut ini
Jawab
02. Uraikanlah bentuk faktorial berikut ini:
Permutasi adalah proses pencacahan yang memperhatikan urutan atau formasi.
Sebagai contoh diketahui himpunan P = {a, b, c, d}. Jika anggota himpunan P tersebut disusun dua-dua maka diperoleh himpunan yang anggotanya sebanyak 12 buah, yakni {ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc}. Banyaknya anggota himpunan ini dapat pula ditentukan dengan aturan permutasi, yakni :
Jika n objek berlainan disusun r objek maka banyak susunannya dapat ditentukan dengan rumus :
Untuk soal diatas banyaknya anggota himpunan P adalah n = 4 dan disusun dua-dua berarti r = 2, sehingga :
Jika yang disusun adalah seluruh anggota himpunan (n = r) maka banyaknya susunan dapat ditentukan dengan rumus :
Sebagai contoh empat buah roti yang berlainan akan disusun satu baris diatas meja, maka banyaknya susunan dapat ditententukan dengan cara :
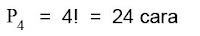
Jika diantara objek yang disusun ada objek-objek yang sama, maka banyaknya formasi susunan dapat ditentukan dengan aturan :
Dimana
n1, n2, n3, … , nk adalah banyaknya masing-masing unsur yang sama.
Sebagai contoh banyaknya cara menyusun enam huruf dari huruf-huruf pada kata PANGAN adalah
Sedangkan n objek berlainan disusun r objek dimana objek-objek tersebut boleh muncul berulang, maka banyaknya susunan yang dapat dibentuk dapat ditentukan dengan rumus
Sebagai contoh dari anggota himpunan A = {p, q} disusun 6 objek dimana objek-objek tersebut boleh muncul berulang. Maka banyaknya susunan seluruhnya adalah …
Jika n objek disusun n objek seluaruhnya, dimana formasi susunan dibuat melingkar (siklis) maka banyak susunan yang dapat dibentuk adalah
Pn = (n – 1) !
Sebagai contoh enam tangkai bunga yang berlainan disusun melingkar diatas meja, maka banyaknya cara menyusunnya adalah :
P6 = (6 – 1)! = 5! = 120
Untuk lebih lengkapnya ikutilah contoh soal berikut ini :
03. Terdapat 8 orang juru masak di suatu restoran. Dari 8 orang ini ditunjuk secara acak 3 orang untuk memasak gulai rendang, sayur lodeh dan sambal daging. Tentukanlah banyaknya cara penunjukan tersebut
Jawab
n = 8 dan r = 3, maka
maka :
04. Tentukanlah banyaknya susunan 8 huruf dari huruf-huruf pada kata “MATAKAKI”
Jawab
05. Didalam sebuah rak terdapat delapan buku matematika yang terbagi ke dalam 3 kelompok bahasa, masing-masing tiga berbahasa Indonesia, tiga berbahasa Inggris dan 2 berbahasa Jerman. Buku-buku itu akan dibagikan kepada 7 orang siswa. Jika buku-buku berbahasa sejenis adalah sama, maka tentukanlah banyaknya cara pembagian tersebut
Jawab
06. Suatu paket soal pilihan ganda sebanyak 4 nomor dengan pilihan jawaban A, B, C, D, dan E. Jika siswa diminta menyilang salah satu pilihan yang dianggap paling benar, maka tentukanlah banyaknya formasi jawaban
Jawab
n = 5 dan r = 4
07. Empat buah kursi a, b, c dan d akan disusun mengelilingi sebuah meja. Tentukanlah banyaknya susunan keempat kursi tersebut
Jawab
n = 4, r = 4 dan formasi melingkar
maka :
P = (4 – 1)! = 3! = 3 x 2 x 1 = 6 susunan
n! = n (n - 1) (n - 2) (n - 3) … 3. 2. 1
Dan nol faktorial didefinisikan sebagai 0! = 1
Sebagai contoh
01. Hitunglah setiap nilai faktorial berikut ini
02. Uraikanlah bentuk faktorial berikut ini:
Permutasi adalah proses pencacahan yang memperhatikan urutan atau formasi.
Sebagai contoh diketahui himpunan P = {a, b, c, d}. Jika anggota himpunan P tersebut disusun dua-dua maka diperoleh himpunan yang anggotanya sebanyak 12 buah, yakni {ab, ac, ad, ba, bc, bd, ca, cb, cd, da, db, dc}. Banyaknya anggota himpunan ini dapat pula ditentukan dengan aturan permutasi, yakni :
Jika n objek berlainan disusun r objek maka banyak susunannya dapat ditentukan dengan rumus :
Sebagai contoh empat buah roti yang berlainan akan disusun satu baris diatas meja, maka banyaknya susunan dapat ditententukan dengan cara :
Jika diantara objek yang disusun ada objek-objek yang sama, maka banyaknya formasi susunan dapat ditentukan dengan aturan :
Dimana
n1, n2, n3, … , nk adalah banyaknya masing-masing unsur yang sama.
Sebagai contoh banyaknya cara menyusun enam huruf dari huruf-huruf pada kata PANGAN adalah
Pn = (n – 1) !
Sebagai contoh enam tangkai bunga yang berlainan disusun melingkar diatas meja, maka banyaknya cara menyusunnya adalah :
P6 = (6 – 1)! = 5! = 120
Untuk lebih lengkapnya ikutilah contoh soal berikut ini :
03. Terdapat 8 orang juru masak di suatu restoran. Dari 8 orang ini ditunjuk secara acak 3 orang untuk memasak gulai rendang, sayur lodeh dan sambal daging. Tentukanlah banyaknya cara penunjukan tersebut
Jawab
n = 8 dan r = 3, maka
maka :
Jawab
05. Didalam sebuah rak terdapat delapan buku matematika yang terbagi ke dalam 3 kelompok bahasa, masing-masing tiga berbahasa Indonesia, tiga berbahasa Inggris dan 2 berbahasa Jerman. Buku-buku itu akan dibagikan kepada 7 orang siswa. Jika buku-buku berbahasa sejenis adalah sama, maka tentukanlah banyaknya cara pembagian tersebut
Jawab
06. Suatu paket soal pilihan ganda sebanyak 4 nomor dengan pilihan jawaban A, B, C, D, dan E. Jika siswa diminta menyilang salah satu pilihan yang dianggap paling benar, maka tentukanlah banyaknya formasi jawaban
Jawab
n = 5 dan r = 4
07. Empat buah kursi a, b, c dan d akan disusun mengelilingi sebuah meja. Tentukanlah banyaknya susunan keempat kursi tersebut
Jawab
n = 4, r = 4 dan formasi melingkar
maka :
P = (4 – 1)! = 3! = 3 x 2 x 1 = 6 susunan
0 komentar
Posting Komentar